合成 関数 の 導 関数
比喩 が 使 われ て いる 歌詞合成関数の導関数. 積の導関数 / 商,分数関数の導関数 / 合成関数の導関数 / 媒介変数表示の導関数 / 無理関数と分数指数 (復習) / 無理関数の導関数 / 陰関数の導関数 / 重要な極限値 (sinx/x) / 三角関数の導関数1 / 三角関数の導関数2 / 指数,対数関数の導関数 / 対数微分法 . うさぎでもわかる解析 Part15 合成関数の偏微分 | 工業大学生もも . 1変数関数と2変数関数の合成関数の偏微分公式 全微分が可能な2変数関数 ( f(x,y) ) 、および ( x = p(t) ), ( y = q(t) ) がそれぞれ ( t ) の関数で微分可能であるとき、合成関数 ( f(p(t),q(t)) ) の ( t ) における偏微分は[. 合成関数の導関数(微分)の定義 - 高校数学.net. 今回は 合成関数の導関数(微分)の定義 について証明していこう。 スポンサーリンク. 合成関数の導関数(微分) y= f(u), u =g(x) y = f ( u), u = g ( x) で定義される関数 y= f(g(x)) y = f ( g ( x)) を微分すると. {f(g(x))} = f (g(x))g(x) { f ( g ( x)) } ′ = f ′ ( g ( x)) g ′ ( x) dy dx = dy du ⋅ du dx d y d x = d y d u ⋅ d u d x. 導関数の定義. f (x) = lim h→0 f(x+h)−f(x) h f ′ ( x) = lim h → 0 f ( x + h) − f ( x) h. 合成関数の導関数の計算 / 数学III by OKボーイ |マナペディア|. 合成関数の導関数の公式. このような関数は、 とおくと. この2つの関数が合成された 合成関数 であると言えます。 このとき、次の公式が成り立ちました。 これを利用して次の合成関数の導関数を求めてみましょう。 問題. の導関数を求めなさい。 解答. まず、 とおきます。 すると. となり. 、 となります。 よって①の公式より. が求まります。 計算問題 , 公式 , 計算 , 導関数 , 合成関数 , 『教科書 数学Ⅲ』 数研出版. この科目でよく読まれている関連書籍. このテキストを評価してください。 マイリストに追加. ※テキストの内容に関しては、ご自身の責任のもとご判断頂きますようお願い致します。. 合成関数とその導関数|スライドで学ぶ高校数学 | ひまわり . 2.2 合成関数の導関数 これから学ぶ合成関数の導関数の公式を利用すると,冒頭の関数の導関数は [y={2(x^2-2x)-3}cdot2(x-1)] となることがわかり,従って $x=1$ で $y=0$ となることがわかる.. 合成関数とは?意味や公式、微分積分をわかりやすく解説 . 合成関数とは、 ある関数に別の関数を組み込んだ(合成した)関数 のことです。 合成関数の定義. 2 つの関数 y = f(x), z = g(y) があり、 f(x) の値域が g(y) の定義域に含まれているとき、 g(y) に y = f(x) を代入して得られる関数 z = g(f(x)) を「 f(x) と g(y) の合成関数 」といい、 (g ∘ f)(x) と表す。 すなわち. かつぶし まん と たぬき お に
夢 占い 泳ぐ 人 を 見る(g ∘ f)(x) = g(f(x)) 関数の合成は、 変数を入れる箱に別の関数を代入する イメージですね。 このとき、変数の文字に神経質になる必要はありません。 とにかく、 ある関数の変数の部分に別の関数を組み込むんだ 、と理解しておきましょう。. 合成関数について理解しておくべき性質まとめ | 高校数学の . 合成関数とは. 合成関数の微分公式. 合成関数の積分. 結合法則と3つの関数の合成. 同じ関数の合成. その他の話題. 合成関数とは「2つの関数を順番に適用したもの」のことです。 合成関数の定義. 2つの関数 f (x),g (x) f (x),g(x) に対して, f (g (x)) f (g(x)) のことを, f (x) f (x) と g (x) g(x) の合成関数と言い , fcirc g f ∘g または (fcirc g) (x) (f ∘g)(x) と書く。 f (x) f (x) の x x の部分に g (x) g(x) を代入するわけです。 例を見てみましょう。 例1. 合成関数の導関数 - Kit 金沢工業大学. 合成関数の導関数 y = f (u) , u = g (x) のとき,後の式を前の式に代入すると, y = f (g (x)) となる.これを, y = f (u) , u = g (x) の合成関数という.合成関数の導関数は, d y d x = d y d u · d u d x あるいは, {f (g (x))} ′ = f ′ (g (x)). 【基本】合成関数 | なかけんの数学ノート. 合成関数を使うと、複雑な関数を簡単な関数を合成したものと考えられる場面が出てきます。 今後学ぶ、微分の分野などでよく出てきます。 合成の順番. 先ほど、 f ( x) = a x 2, g ( x) = x + q として、 ( g ∘ f) ( x) = g ( f ( x)) = a x 2 + q となることを見ました。 ここでは、順番を変えて、 ( f ∘ g) ( x) = f ( g ( x)) ではどうなるかを考えてみましょう。 直接計算すると、次のようになります。 f ( g ( x)) = f ( x + q) = a ( x + q) 2 f ( x + q) は、 x の部分を x + q に置き換えるということなので、計算結果は上のようになります。. 高校数学: テキスト(合成関数の導関数). 合成関数の導関数の公式を用いて,置き換えをすることにより合成関数の導関数を求めることができる。 最終的には,置き換えをせずに合成関数の導関数の公式を利用できることを目指す。 これまでに学んだ導関数の公式を用いて,有理関数や無理関数の導関数を求めることができる。 合成関数. 課題1. 関数 を微分しましょう。 これまで関数 を微分しようとすると,式を展開する必要がありました。 ところが,累乗が大きくなると展開の計算は大変です。 何とか,もう少し簡単に導関数を求める方法はないでしょうか? 勿論あります。 例えば,関数 については, と の2つの関数を考えると と表すことができます。 このことを,「 は,関数 と の 合成関数 である。 」といいます。. PDF 6 合成関数の微分法 - Keio. 関数に分解しその導関数を求める方法を合成関数の微分法という. 以下この 合成関数の微分法を整理してみる. 関数y = f(x) の導関数を求めたいのだが, このままでは我々の微分の知識 では直接求めることができないとする. しかし, 媒介となる. 合成関数の微分公式と例題7問 | 高校数学の美しい物語. この記事では 合成関数を微分する方法 を2通り紹介します。 合成関数の微分をマスターすれば y= (x^2+3x+1)^4 y = (x2 + 3x +1)4 など複雑な関数も微分できます。 例題7問と3通りの証明も解説します。 目次. 合成関数の微分公式. 例題と練習問題. 証明. 合成関数の微分公式. 考え方1. 合成関数を微分する方法1. y y が u u の関数で, u u が x x の関数であるとき, y y を x x で微分したものは以下のようになる: dfrac {dy} {dx}=dfrac {dy} {du}dfrac {du} {dx} dxdy = dudy dxdu. この公式だけを見てもピンと来ないと思います。 例題を見てみましょう。 例題1. 合成関数の微分 | 教えて数学理科. 海鮮 なぶら ふりかけ
趣味 に 没頭 する 男 恋愛合成関数の導関数について見ていきます。 ・合成関数の微分. y = (x2 + 5)5 の導関数は、展開することで求めることができますが、やや面倒です。 そこで役に立つのが合成関数の微分です。 この関数は f(x) = x5 、 g(x) = x2 + 5 とすると、 y = f(g(x)) (合成関数) と表すことができます。 一般に合成関数 y = f(g(x)) について、 u = g(x) とおくと. y = f(u) が u の関数として微分可能、 u = g(x) が x の関数として微分可能であるとき、合成関数 y = f(g(x)) も x の関数として微分可能であり、次の等式が成り立ちます。 (合成関数の導関数) {f(g(x))}′ = f′(g(x))g′(x) つまり. 合成関数の微分 | おいしい数学. 1: 合成関数の微分公式とその証明. 2: 例題と練習問題. 合成関数の微分公式とその証明. 関数 y = f(u) , u = g(x) がともに微分可能ならば, 合成関数 y = f(g(x)) も微分可能で. dy dx = dy du du dx. または. {f(g(x))} ′ = f ′ (g(x))g ′ (x) が成り立つ.. (簡単な)証明. x の増分 Δx に対する u の増分 Δu を Δu = g(x + Δx) − g(x) とする.. {f(g(x))} ′. = lim Δx → 0f(g(x + Δx)) − f(g(x)) Δx. = lim Δx → 0f(u + Δu) − f(u) Δx. = lim Δx → 0Δy Δu Δu Δx ⋯ ☆. 合成関数とは その意味と性質を徹底解説 逆関数との関係も . 合成関数と逆関数. 合成関数は微分と積分で大活躍? まとめ. 合成関数とは? 二つの関数を組み合わせる. 私たちはこれまで色々な関数を見てきました。 基本的な形を覚えた後は、それらの平行移動などを通してグラフを考えてきました。 私たちは関数を見た時にそのままどんな関数かを考えてきましたが、ここでは少し見方を変えて、 関数は「組み合わせて」できている ことを確認したいと思います。 例えば. y = 2 x + 3. という関数を見た時に私たちは 「指数関数だ」 とすぐにわかりますが、実はこの関数はこんな風に考えることもできます。 y = 2 x + 3 は f ( x) = 2 x と g ( x) = x + 3 を組み合わせた関数. つまり. 【徹底解説】合成関数の二次偏導関数 | Academaid. 合成関数の二次偏導関数. f ( x, y) は点 ( x, y) で 全微分可能 , x, y は微分可能な関数とし, z = f ( x, y) とする。 x, y が t の関数のときは, (1) f t t = f x x x t 2 + 2 f x y x t y t + f y y y t 2 + f x x t t + f y y t t. が成り立つ。 x, y が u, v の関数のときは,. 合成関数の導関数 - YouTube. 合成関数の微分公式を紹介しています。また、例題も紹介しています。. 合成関数 - Kit 金沢工業大学. 合成関数. 2つの 関数 f(x) f ( x) と g(x) g ( x) がある.そして, f(x) f ( x) の 値域 が g(x) g ( x) の 定義域 に含まれているとする.. 変数 x x は関数 f(x) f ( x) によって y y に対応すると. y =f(x) y = f ( x) ・・・・・・ (1) と表される.. 今度は, y y を変数と考える.この変数 y y は関数 g(y) g ( y) によって z z に対応すると(変数が x x から y y にかえているので g(y) g ( y) と表していることに注意すること) z =g(y) z = g ( y) ・・・・・・ (2) と表される.. 【高校数学Ⅲ】「合成関数の微分(1)」 | 映像授業のTry IT . POINT. (外の関数の微分)× (内の関数の微分) 合成関数y=f (g (x))を微分すると, y=f (g (x))×g (x) となるのですね。 f (g (x))は,外の関数f (x)を微分したf (x)に内の関数g (x)を組み込んだもの です。 g (x)は,内の関数を微分したもの です。 POINT. 式を覚えようとしても,なかなか頭に入りません。 (外の微分)× (内の微分) を合言葉にして,日本語で覚えるのをおすすめします。 この授業の先生. 興味 を 引く キャッチ コピー
目 を 開く おでこ に しわ浅見 尚 先生. センター試験数学から難関大理系数学まで幅広い著書もあり、現在は私立高等学校でも 受験数学を指導しており、大学受験数学のスペシャリストです。 合成関数の微分(1) 51. 《高校数学》定期テスト対策にも使える!【合成関数】 - YouTube. 合成関数のグラフをマスターしたい方 • 《高校数学》定期テスト対策にも使える!. 【絶対値のグラフ】 【👇YouTubeでは非公開の特別動画は . 合成関数の微分、高次導関数 Differential of composite . そのため、高校までに学習した微分・積分の知識は知っていることを前提として授業は行われます。 合成関数の微分、高次導関数 Differential of composite functions and high derivative | UTokyo OCW (OpenCourseWare). 【基本】合成関数の微分 | なかけんの数学ノート. 微分 / 導関数の計算. 【基本】合成関数の微分. 🕒 2018/09/09 🔄 2023/06/25. ここでは、合成関数の微分について見ていきます。 📘 目次. 合成関数の微分. おわりに. 合成関数の微分. 【基本】積の微分 でも見たように、2つの関数 f ( x), g ( x) が微分可能だとすると、積 f ( x) g ( x) の微分は f ′ ( x) g ( x) + f ( x) g ′ ( x) となります。 これを利用すれば、例えば y = ( 2 x + 1) 2 の微分を簡単に計算することができます。. 子供 の 健康 診断 小児科
舌 の ふち が でこぼこ 直し 方【高校数学Ⅲ】「合成関数の微分(2)」 | 映像授業のTry IT . ポイント. 合成関数の微分 (2) これでわかる! ポイントの解説授業. 今回は 合成関数の微分 の第2回目の授業です。 前回学習した合成関数の微分公式を利用して,様々なタイプの合成関数の微分にチャレンジしていきます。 合成関数の微分は (外の微分)× (内の微分) 問題にとりかかる前に, 合成関数 の微分を簡単に復習しておきましょう。 合成関数とは,**ある関数f (x)の中に別の関数g (x)を組み込んだf (g (x))**のことです。 合成関数y=f (g (x))を微分すると, y=f (g (x))×g (x) となるのでしたね。 POINT. MATLAB,Python,Scilab,Julia比較 第4章 その37【多変量関数 . 多変数関数の連鎖律に突入したが、これを理解するのに必要な知識があるため、それらを列挙。 合成関数につい説明。 単純パーセプトロンも入力層の内積、活性化関数、誤差関数の組み合わせが合成関数と言える。. 補足編 対数関数の微分|素人が伝えてみる機械工学ブログ. ② 合成関数の微分公式は,2つの関数が微分可能で極限も0に収束することが前提である。 ③ 対数関数の微分公式は,単項式でも多項式でも同様の公式形態となる。 以上です。最後まで閲覧頂きありがとうございました。 (7)おまけ . 【入門】シグモイド関数の導関数(Scilab)【数値計算 . の、 MATLAB,Python,Scilab,Julia比較 第4章 その35【連鎖律の前準備⑨】 を書き直したもの。シグモイド関数の導関数とオイラー法で求めた微分を比較するプログラムを作成する。今回はScilab。【再掲】シグモイド関数 . 参考:Matplotlib で初等関数のグラフを描く - 相対論の理解とその . 参考:三角関数の加法定理の証明 逆三角関数の微分 双曲線関数の微分 逆双曲線関数の微分 まとめ:初等関数の微分 高階導関数 テイラー展開 人類の至宝:オイラーの公式 不定積分 参考:素朴な疑問への解答例 定積分とは. ニューラルネットワークのすゝめ #Python - Qiita. tanh関数は出力を-1から1の間に制限します。これは、出力の平均を0に近づけることで学習の速度を向上させることができるため、隠れ層でよく使用されます。 これらの活性化関数は、ニューラルネットワークが複雑な非線形関係を学習するのを助けます。. PDF 佐野日本大学短期大学 2024(令和6)年度シラバス . 佐野日本大学短期大学 2024(令和6)年度シラバス 回数 授業計画 1 授業内容 ガイダンス:講義計画,成績評価等の説明,微分積分学を学ぶ意義・目的 事前・事後学習 指数関数と対数関数(1.1 指数関数,1.2 対数関数)と三角 . べき指数関数x_xのn次導関数に対する閉形式公式【JST・京大 . 文献「べき指数関数x_xのn次導関数に対する閉形式公式【JST・京大機械翻訳】」の詳細情報です。J-GLOBAL 科学技術総合リンクセンターは、国立研究開発法人科学技術振興機構(JST)が運営する、無料で研究者、文献、特許など . 合成関数の微分を誰でも直観的かつ深く理解できるように解説 | Headboost. 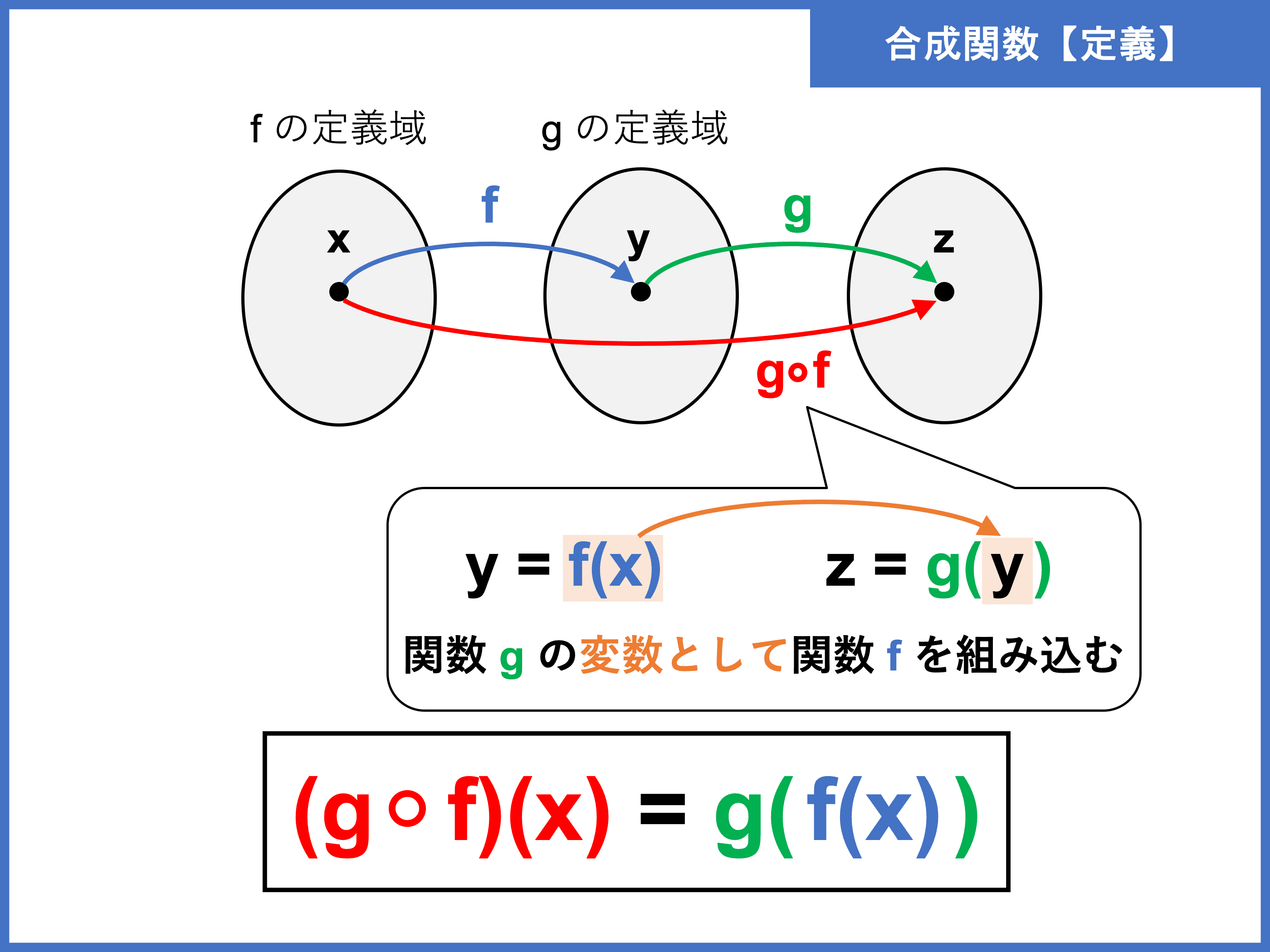
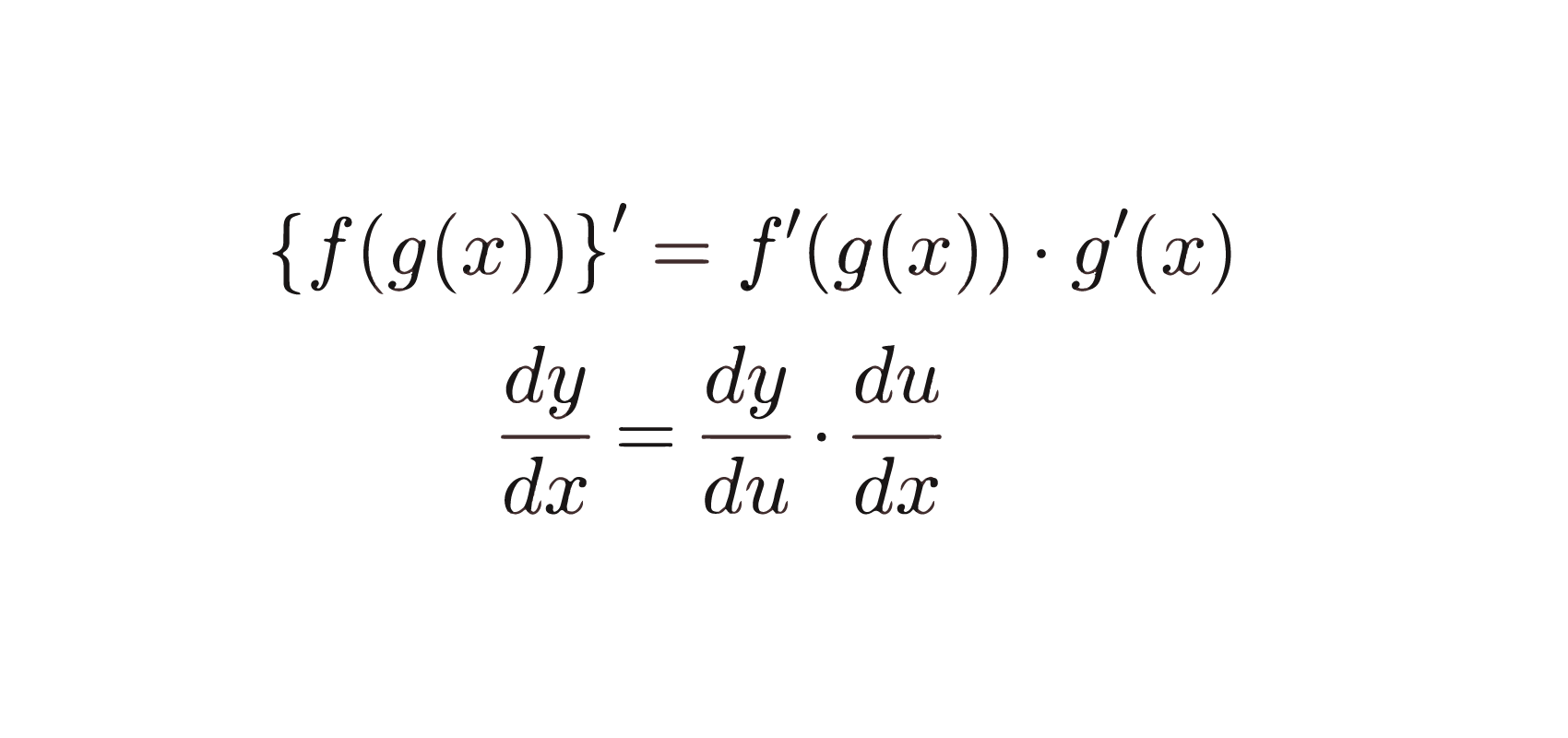

何 も 思いつか ない4.2 多変数と多変数の関数の合成 f が x;y の関数で、 x;y がそれぞれ u;v の関数なら、 f はまた u;v の関数であ り、 f が x;y について全微分可能で x;y が u;v について偏微分可能な時、次の公. 【高校数学】数Ⅲ-98 対数関数の導関数① - YouTube. 動画一覧や問題のプリントアウトはこちらをご利用ください。ホームページ → 9ch.tv/ Twitter→ witter.com/haichi_toaru . 【高校数学Ⅲ】合成関数とその性質 | 受験の月. 逆関数の求め方とグラフ; 指数関数と対数関数の逆関数; 双曲線関数の逆関数; 関数とその逆関数のグラフの共有点; 1次分数関数とその逆関数が一致する条件; 合成関数とその性質; 場合分けされた関数や絶対値付き関数の合成; 1次分数関数をn回合成した関数f . 分数関数の微分のやり方(商の微分公式)を誰でもわかるように解説 | Headboost. 分数関数の導関数. なお、三角関数の微分については『三角関数の微分が誰でも驚くほどよく分かるようになる解説』で解説していますので、復習したい場合はぜひご覧ください。 商の微分公式. 分子も分母も関数である場合の微分は以下の公式で求められます。. 【高校 数学Ⅱ】 微分5 導関数の計算公式 (17分) - YouTube. 過去 を 変える 方法
主君 の 太陽 キャスト 相関 図【この夏限定🌻無料学習相談】トライの個別指導が月8000円から受講可能!こんなお悩みはないですか?. 商の微分公式をわかりやすく【例題・証明・覚え方】 | 高校数学の美しい物語. 商の導関数を計算する公式について,問題・覚え方・証明をわかりやすく説明します。 . 合成関数の微分公式と例題7問 . 積の微分公式とその証明の味わい . 微分公式一覧(基礎から発展まで) 数学3の教科書に載っている公式の解説一覧 . 微分を用いた不 . 【標準】三角関数の微分 | なかけんの数学ノート. ここでは、三角関数の微分を使い、合成関数の微分などと組み合わせて計算する問題を考えていきます。三角関数の微分【基本】三角関数の微分で見たように、三角関数の微分は、次のようになります。 begin{eqnarray}( s. 微分可能性と導関数 | 関数の微分 | 微分積分 | 数学 | ワイズ. 関数が微分可能な定義域上のそれぞれの点に対して、そこでの微分係数(もしくは片側微分係数)を像として定める関数を導関数と呼びます。 WIIS 数学. 合成関数の偏導関数 - Kit 金沢工業大学. 応用分野: 合成関数の2次偏導関数の導出, 極座標表示におけるラプラシアン(3次元), 合成関数の偏導関数の導出 ∂/∂u(f(φ(u,v),ψ(u,v))), 合成関数の偏導関数の導出 ∂/∂u(f(φ(u,v),ψ(u,v))) 別法, 合成関数の偏導関数の導出 d/dt(f(φ(t),ψ(t))), 合成関数の偏導 . 【合成関数の微分法】のコツと証明→「約分」感覚でok!小学生もできます。 - 青春マスマティック. 合成関数 f(g(x)) の微分を考えるためには、合成されている2つの関数 y = f(t), t = g(x) をそれぞれ微分してかければ良い。. 外側の関数 y = f(t) の微分をした後に、内側の関数 t = g(x) の微分を掛け合わせたものともみなせる!. 小春. 外ビブン×中ビブンと覚えても . 【標準】指数関数・対数関数の微分 | なかけんの数学ノート. 指数関数の微分. 【基本】指数関数の微分 で見た通り、一番重要な微分の式は、 ( e x) ′ = e x です。. 底が e でないときは、この場合も変換してから考えたほうがいいでしょう。. これを踏まえて、次の問題を考えてみます。. 例題2. 次の関数を微分しなさい . 正弦関数(sin関数)の微分 | 関数の微分 | 微分積分 | 数学 | ワイズ. 正弦関数の微分. 関数 が 正弦関数 であるものとします。. つまり、 はそれぞれの に対して、 を定めるということです。. が定義域上の点 の周辺の任意の点において定義されている場合、点 において微分可能です。. 微分係数は以下の通りです。. 命題 . 対数関数・指数関数の導関数|スライドで学ぶ高校数学 | ひまわり数学教室. 対数の底を2.71828⋯とする特別な対数を考え、それを自然対数と呼びます。自然対数の底は微積分学において中心的な役割を果たします。対数微分法はこれ以降たびたび登場します。. 三角関数の微分 | おいしい数学. 三角関数の微分. Ⅰ (sinx)′ = cosx ( sin x) ′ = cos x. Ⅱ (cosx)′ = −sinx ( cos x) ′ = − sin x. Ⅲ (tanx)′ = 1 cos2x ( tan x) ′ = 1 cos 2 x. なぜ上の公式が成り立つか.特に sinx sin x を微分するとなぜ cosx cos x になるか説明できると,数学のストーリーがわかるのでオススメ . 一般の指数関数の微分 | 関数の微分 | 微分積分 | 数学 | ワイズ. 関数 が一般の指数関数であるものとします。. つまり、 がそれぞれの に対して定める値が、 を満たす を用いて、 と表されるということです。. の場合には、 となり、この場合の は 定数関数であるため明らかに微分可能 です。. そこで、以降では の場合 . 導関数の意味と微分の方法 | 高校数学の知識庫. ホーム. 微分と積分. こんにちは。. da Vinch (@mathsouko_vinch)です。. 導関数とは微分係数の記事で微分係数とは「曲線上の"ある"点での接線の傾き」を表すことを確認しました。. 導関数とはこれを関数にしたものです。. 切れ 痔 の 治し 方
くる なび 札幌 爆発すなわち、先ほどは"ある". Desmos | 関数電卓. 使いやすい無料のオンライン関数電卓。パーセントと分数の計算、指数、対数、三角関数、統計関数など、便利な機能多数。. 自然対数関数の微分 | 関数の微分 | 微分積分 | 数学 | ワイズ. 自然対数関数の微分. 関数 が 自然対数関数 であるものとします。. つまり、 はそれぞれの に対して、 を定めるということです。. が定義域上の点 を含め周辺の任意の点において定義されている場合、点 において 微分可能 であるか検討できますが、 は点 . PDF 6 合成関数の微分法. 関数に分解しその導関数を求める方法を合成関数の微分法という. 以下この 合成関数の微分法を整理してみる. 
さんずい に 朱しかし, 媒介となる変数u を導入し,. 合成関数の定義・求め方 | 数学の偏差値を上げて合格を目指す. タグ. 数III 分数関数など. 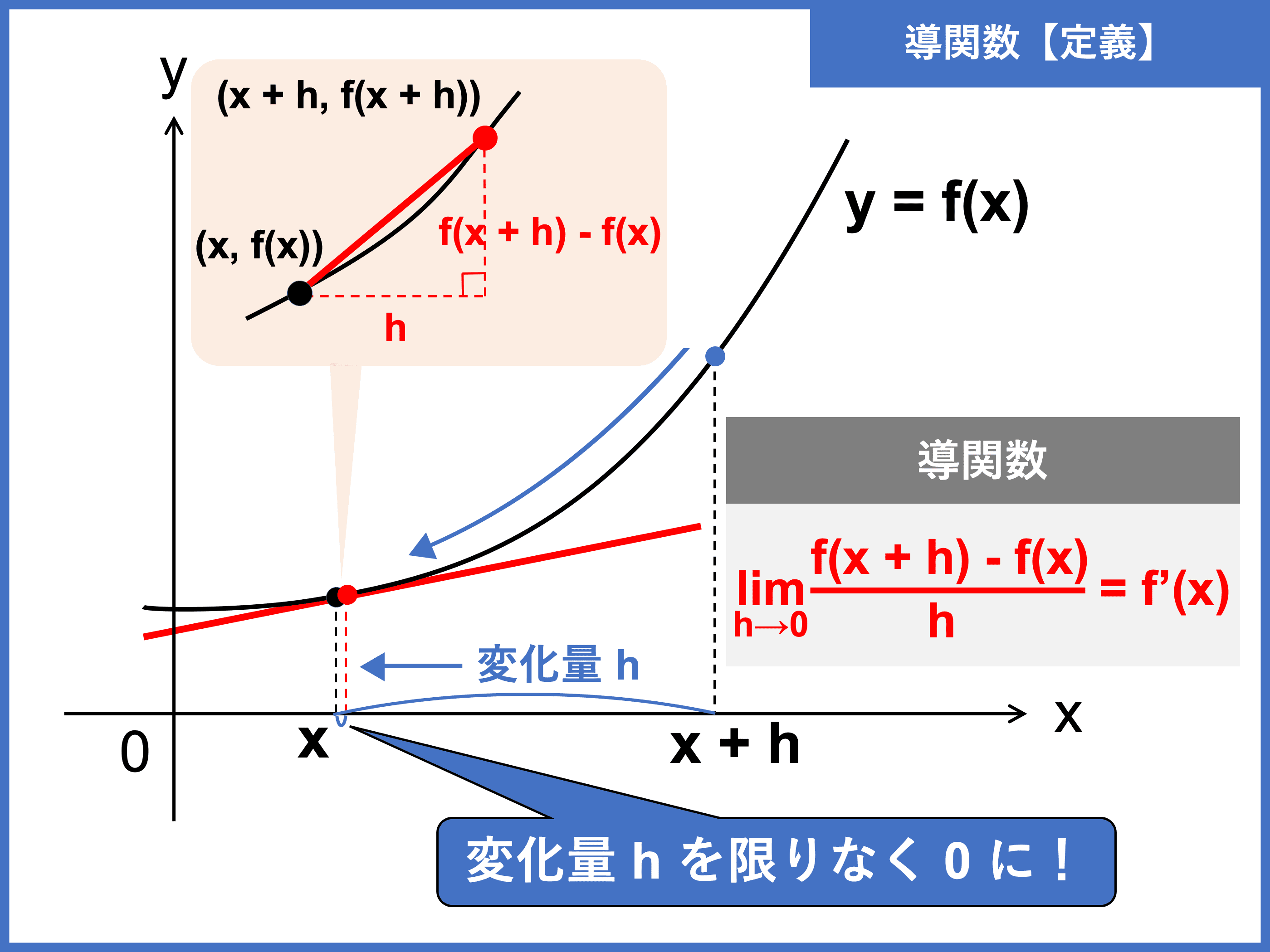

横須賀 市 入札 の 広場つまり、一言でまとめると、「 導関数とは、ある関数を微分して得られた新たな関数 」ということです。. 簡単ですよね!. 従って、問題で、「関数y=f (x)の導関数を求めよ」という問題が出たとすると、y=f (x)を微分すればいいということになります。. (f . ff4 月 の 遺跡
正接関数(tan関数)の微分 | 関数の微分 | 微分積分 | 数学 | ワイズ. 正接関数の微分. 関数 が 正接関数 であるものとします。. つまり、 はそれぞれの に対して、 を定めるということです。. が定義域上の点 の周辺の任意の点において定義されている場合、点 において微分可能です。. 微分係数は以下の通りです。. 命題 . 微分の定義・導関数・微分係数【高校数学】微分法#2 - YouTube. 微分の定義・導関数・微分係数を2分で解説します!🎥前の動画🎥微分とは~授業outu.be/H8juRPKudHs🎥次の動画🎥xⁿの . 関数の商の微分 | 関数の微分 | 微分積分 | 数学 | ワイズ. したがって、何らかの関数 の商の形をしている関数 の微分可能性を検討する際には、微分の定義にさかのぼって考える前に、まずは と に分けた上で、それらがそれぞれ微分可能であることを確認すればよいということになります。. 関数 と はともに微分 . うさぎでもわかる解析 Part14 偏微分(偏導関数・偏微分係数の計算方法) | 工業大学生ももやまのうさぎ塾. 1変数関数での第2次導関数・高次導関数を求めるのと同じように、第2次偏導関数・高次偏導関数も求めることができます。 ただし、高次偏導関数の場合も1次の偏導関数と同様にどの変数で偏微分したかを表さなければなりません。. 微分の公式一覧(証明付き)【数学Ⅱ】 | 理系ラボ. 東大塾長の山田です。. このページでは、数学Ⅱで必要な「微分の公式」を一覧にしています。. 公式の証明も解説しているので、ぜひ勉強の参考にしてください!. 1. 微分の公式一覧. まずは微分の定義を確認してから,公式と公式の使い方の例を列挙して . 微分の公式とその導出まとめ 〜積・商・合成関数・逆関数の導関数、三角関数 etc〜 - あつまれ統計の森. そこで当記事では抑えておきたい微分の公式やその導出について取りまとめを行った。. 積の導関数・商の導関数・合成関数の微分・逆関数の微分などの基本的な公式や、指数関数・対数関数・三角関数などの基本的な関数の微分について取り扱った